B-Tree/B+Tree

Q . 

- DB의 Index 구현체로 자주 사용되는 자료구조

- B-Tree와 B+Tree의 차이점

 

 

B-Tree(Balanced Tree)

 - 리프 노드들이 같은 레벨을 가질 수 있도록 편향되지 않는 트리(균형 이진 트리의 확장)

 - 이진 트리와 달리 2개 이상의 자식을 가질 수 있음(하나의 노드에 3개의 자식)

 - 하나의 노드에 여러 정보(key)를 담을 수 있음

    - 차수 : 하나의 노드가 가질 수 있는 자식 노드의 수 (차수가 N -> N차 B-Tree)

 

https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Tree

 

    -> 하나의 블럭에 여러 자료(key)를 담기 때문에 더 많은 데이터를 저장소에 효율적으로 저장할 수 있음

 

하드디스크와 같은 외부 저장장치는 블럭 단위로 파일을 입출력하고, 이 때 입출력의 비용은 블럭 안의 파일 크기와는 상관 없이 블럭 단위로 정해진다.

-> 하나의 블럭에 1byte파일/1000byte파일 저장되어 있든 둘의 비용은 차이가 없음

=> 하나의 블럭에 여러 데이터들을 동시 저장할 수 있다면 보다 효율적으로 사용이 가능함.

 

 

특징

 - 각 노드의 자료(key)들은 정렬되어 있음(중위)

 - key들은 중복되지 않음

 - 모든 리프 노드들은 같은 레벨(균형 트리)

 - N차 트리에서, leaf 노드가 아닌 노드들은 적어도 N/2개의 자식 노드를 가짐

 

 

 

 

 

key 삽입

if) 3차 B-Tree

 - 한 노드에 삽입될 수 있는 key의 수 최대 2개

 - 자식 노드 최대 3개 

 

1. 삽입에 적절한 리프 노드를 검색하고, 2. 필요한 경우(최대 key의 수 초과) 리프 노드를 분할

 

1) 분할이 일어나지 않을 때(리프 노드가 차지 않을 때)

 

 

7 삽입

 

루프에서부터 삽입될 위치 탐색

 

2) 분할이 일어날 때

 

 

6 삽입

한 노드가 가질 수 있는 최대 key의 개수를 초과

 

 

 

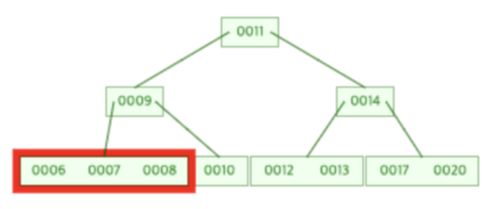
노드의 분할 과정 이루어 짐

 

중앙값(7)은 부모 노드로 병합

6,7,8 key값을 갖고 있던 노드가 분할되고, 

7 노드가 부모 노드로 삽입되어 6은 왼쪽 자식 노드, 8은 오른쪽 자식 노드로 설정됨

 

 

 

 

 

key 삭제

 

1) 삭제할 key가 leaf 인 경우

1-1) 트리 균형 조정이 필요하지 않은 경우

key가 삭제된 후 노드의 key개수가 최소 key개수보다 클 때

 

 

12 삭제

 

 

 

 

1-2) 균형 조정이 필요한 경우

삭제 후 노드의 key개수가 최소 개수에 도달하지 못할 때

 

1. 삭제되는 key의 자리와 부모key의 자리를 바꿈 

2. 삭제 후 기존의 (왼쪽 형제 노드에서 가장 큰/오른쪽 형제 노드에서 가장 작은) 값으로 부모 key 위치를 대체함

 

 

 

13 삭제

13과 그의 부모key인 14가 교체되고(1)

 

기존 위치의 오른 형제 노드에서 가장 작은 값인 17이 부모key를 대체

 

 

 

 

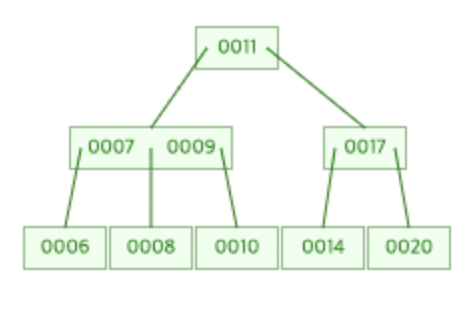
2) 삭제할 key가 leaf노드가 아닌 경우

inorder predecessor : 노드의 왼쪽 자손에서 가장 큰 key

inorder successor : 노드의 오른쪽 자손에서 가장 작은 key

 

1. 현재 노드의 inorder predecessor/inorder successor (leaf node)와 삭제할 key의 자리를 바꿈

2. 삭제 후, 리프 노드의 삭제에서처럼 트리의 균형 조정 실행됨

 

 

11 삭제

 

 

 

inorder predecessor(노드의 왼쪽 자손(트리)에서 가장 큰 key)

 

위치 변환(1)

 

트리 균형 조정(2)

 

 

 

B+Tree

 

https://rebro.kr/167

 

 B-Tree와의 차이점

 - 노드에 대한 탐색 연산(검색 연산)을 개선한 트리

 - 같은 레벨의 모든 키 값들이 정렬되어 있고, 연결리스트 형태로 이어져 있음 -> 효율적인 순차 탐색

 - leaf node를 데이터 노드, leaf node가 아닌 노드를 인덱스 노드라고 함. 

 - 키 값이 중복될 수 있음(인덱스 노드, 데이터 노드가 따로 존재하므로)

 - leaf node에서만 데이터가 검색되므로, 탐색의 시간복잡도는 항상 O(logN)

 

데이터 노드에만 데이터가 존재하고, 인덱스 노드의 value값에는 다음 노드를 가리키는 포인터 주소가 존재함.

 

 

 

 

---

 

https://velog.io/@emplam27/%EC%9E%90%EB%A3%8C%EA%B5%AC%EC%A1%B0-%EA%B7%B8%EB%A6%BC%EC%9C%BC%EB%A1%9C-%EC%95%8C%EC%95%84%EB%B3%B4%EB%8A%94-B-Tree

[자료구조] 그림으로 알아보는 B-Tree

 

https://ssocoit.tistory.com/217

[자료구조] 간단히 알아보는 B-Tree, B+Tree, B*Tree

 

https://www.cs.usfca.edu/~galles/visualization/BTree.html

B-Tree Visualization